Draft - Bon à savoir
1 Introduction
Ce document reprend des informations utiles non classées, que je cherche souvent dans mes références.
2 Le rayonnement du corps noir
La théorie du « corps noir » a été élaborée par plusieurs physiciens dans la seconde moitié du 19ème siècle pour établir un lien entre le flux de rayonnement émis par tout solide à une température supérieure au zéro absolu et la température de ce solide. La meilleure représentation qu’on puisse se faire du modèle sur lequel est basée cette théorie est celle d’un four sous vide et à l’équilibre thermique dont la paroi interne opaque absorbe, sans aucune réflexion ni transmission, tout rayonnement électromagnétique quelle que soit sa longueur d’onde. A l’équilibre thermique elle doit également réémettre tout rayonnement absorbé. Ce four parfaitement isolé devrait cependant être percé d’un minuscule orifice permettant d’analyser le rayonnement concentré à l’intérieur. Aucune interprétation quantitative du spectre observé ne fut possible dans le cadre de la théorie électromagnétique classique et c’est finalement Planck qui proposa en 1900 une équation introduisant l’idée, révolutionnaire pour l’époque, qu’à chaque longueur d’onde le rayonnement ne peut être émis que sous forme de « quanta » (c’est-à-dire de petits paquets) dont l’énergie est hν = hc/λ (où ν et λ sont respectivement la fréquence et la longueur d’onde du rayonnement, c la vitesse de la lumière et h une nouvelle constante de la nature appelée désormais constante de Planck). Ce rayonnement qualifié de « thermique » est dû à l’oscillation de dipôles électriques formés par le noyau et le nuage électronique des atomes qui, en accord avec les lois de l’électromagnétisme, émettent un rayonnement de fréquence égale à la fréquence d’oscillation.
La luminance énergétique spectrale d’une surface est le flux énergétique émis par la surface par unité d’aire de la surface projetée, par unité d’angle solide, par unité spectrale (fréquence, longueur d’onde, période, nombre d’onde et leurs équivalents angulaires). Elle est donnée par la formule de Planck:
où:
| = La luminance énergétique spectrale | W m-3 sr-1 | |
| = la constante de Planck | 6,626 070 15 10−34 J s | |
| = la vitesse de la lumière | 299 792 458 m s−1 | |
| = la longueur d’onde | m | |
| = la constante de Boltzmann | 1,380 649 10−23 J K−1 | |
| = la température | K |
L’émittance énergétique spectrale s’obtient en intégrant la luminance énergétique spectrale suivant toutes les directions de l’hémisphère dans lequel rayonne un élément de surface. Elle est égale à
L’intégration de l’émittance énergétique spectrale sur tout le domaine de longueurs d’onde conduit à la formule de Stefan-Boltzmann qui lie l’émittance hémisphérique totale E(T) à la température:
où:
| = l’émittance hémisphérique totale | W m-2 | |
| = la constante de Stefan-Boltzmann | 5,670 374 10-8 W m-2 K-4 | |
| = la température | K |
2.1 Le rayonnement émis par le soleil
L’intégrale de la courbe est égale au rayonnement solaire au sommet de l’atmosphère qui peut également être calculé comme suit:
où:
| = le rayonnement solaire au sommet de l’atmosphère | 1 364 W m-2 | |
| = la constante de Stefan-Boltzmann | 5,670 374 10-8 W m-2 °K-4 | |
| = la température de surface du Soleil | 5 780 °K | |
| = le rayon du soleil | 696 342 km | |
| La distance moyenne entre la Terre et le Soleil | 150 000 000 km |
2.2 Le rayonnement émis par la Terre
L’intégrale de la courbe vaut la puissance au sommet de l’atmosphère. Elle est égale à 394 W/m2.
3 Le profil de la température dans l’atmosphère
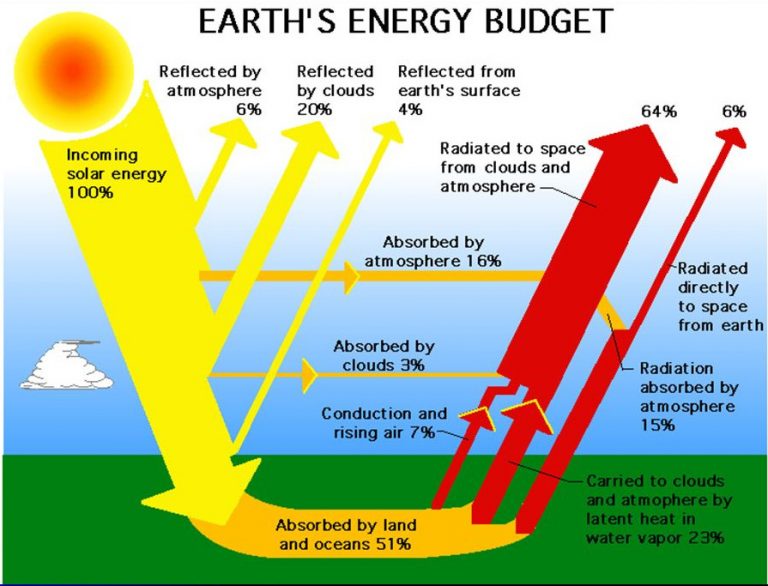
4 Le budget énergétique de la Terre
Le rayonnement solaire entrant est pris égal à 340 W/m2. La Terre a été aplatie et est devenue un disque de même rayon. Comme il y a un rapport de 1 à 4 entre la surface d’un disque et celle d’une sphère de même rayon, le rayonnement moyen sur la Terre est considéré égal au rayonnement solaire incident au sommet de l’atmosphère (1360 W/m2) divisé par 4, soit donc 340 W/m2.
Le rayonnement absorbé par l’atmosphère (16%) et par les nuages (3%) ne revient pas sur Terre, mais ne fait que transiter et est réémis vers l’espace. Ce n’est pas illogique si on considère que l’atmosphère est plus froide que la surface de la Terre.
Le rayonnement absorbé par la surface de la Terre est de 179 W/m2 (0.51 * 340). Il est réémis vers l’espace par convection (7%), vaporisation (23%) et rayonnement (21%).
L’albédo de la Terre est égal à 30% (6% de réflexion par l’atmosphère, 20% par les nuages et 4% par la surface de la Terre). S’il n’y avait pas d’absorption par l’atmosphère et les nuages, le rayonnement absorbé par la surface serait de 238 W/m2.
En se basant sur l’ Eq. 3, certains en déduisent que la température de la surface terrestre devrait être égale à
Ce calcul est complètement faux. Il est effectué avec la puissance moyenne sur le disque, sans tenir compte de l’inertie thermique des sols et des océans. On n’obtient un résultat correct que si le calcul est effectué sur la sphère et que le profil de température est le même quelle que soit la longitude pour tenir compte de l’inertie thermique.
Supposons que quelle que soit la longitude, le profil moyen de température selon un méridien soit de la forme suivante, x représentant la latitude en radians:
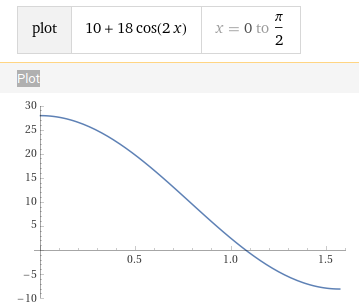
Dans ce profil, la température moyenne à l’équateur est égale à 28 °C et vaut -10 °C aux Pôles.
La moyenne de la température est égale à
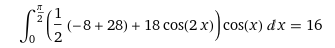
avec une puissance correspondante de 396 W/m2:

Le rayonnement moyen obtenu en appliquant l’Eq. 3 localement est égal à
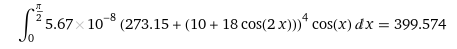
Si on fait le calcul inverse avec cette dernière valeur, on obtient une température correspondante de 16.6 °C.
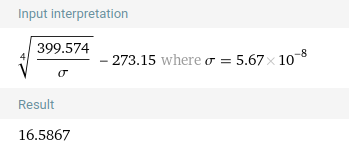
Ces résultats sont très voisins.
Moyennant quelques hypothèses très raisonnables, il est facile de calculer la température moyenne de la surface terrestre sans atmosphère.
Faisons les hypothèses suivantes:
La température en chaque point de la surface est donnée par l’Eq. 3 en fonction du rayonnement solaire incident.
L’albédo de cette Terre sans atmosphère serait identique à celui de la Terre réelle (0.30)
En chaque point, la température moyenne est voisine de la température pendant le jour ou la nuit. Les relevés de température des bouées montrent que l’amplitude thermique journalière n’est que de quelques degrés. C’est dû au fait que l’inertie thermique des océans est énorme. Celle des terres émergées est plus faible, et l’amplitude est plus forte. En l’absence de rayonnement la nuit, la température devrait être égale à 0 °K. Ce n’est jamais le cas, et même dans les déserts, l’amplitude de température entre le jour et la nuit ne dépasse pas 30 °C. De plus, les océans représentent 71% de la surface de la Terre. On peut donc considérer que cette hypothèse ne s’écarte pas beaucoup de la réalité.
Dans ces conditions, la température moyenne de la Terre sera égale à celle calculée sur le demi-hémisphère éclairé. Elle peut être calculée analytiquement. On obtient:
où:
| = la température moyenne | 288 °K | |
| = l’albédo | 0.30 | |
| = le rayonnement solaire au sommet de l’atmosphère | 1 364 W m-2 | |
| = la constante de Stefan-Boltzmann | 5,670 374 10-8 W m-2 °K-4 |
Le résultat est surprenant: le calcul donne une température moyenne égale à celle que l’on observe, soit 15 °C. L’importante inertie thermique et l’albédo suffisent à expliquer la température moyenne observée. Où est passé l’effet de serre de 33 °C ?
En l’absence d’inertie thermique, la température de l’hémisphère non éclairé serait égale à 0 °K, et la température moyenne globale vaudrait 144 °K (-129 °C).
Le détail de cette analyse est présenté dans cette vidéo de Markus Ott.
La Fig. 4 ne contient aucun élément justifiant un effet de serre. Elle n’est plus disponible sur le site de la NASA. Elle a été remplacée par la Fig. 5.
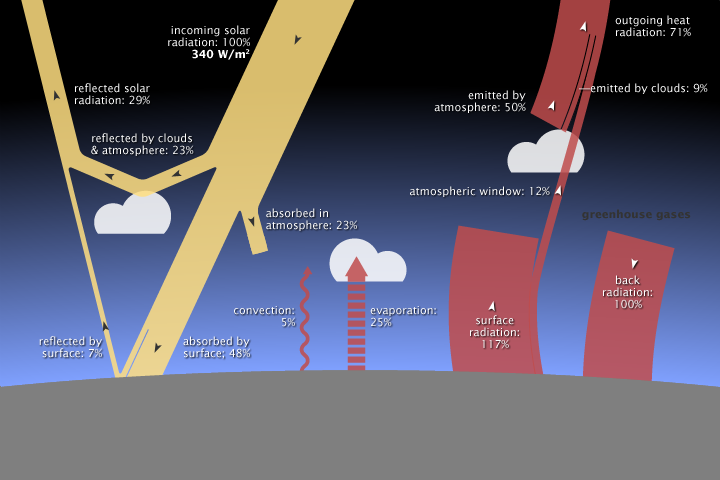
La part de rayonnement solaire absorbé est passée de 51% à 48%, la convection de 7% à 5%, l’évaporation de 23% à 25%, le rayonnement net de surface de 23% à 117% - 100%=17%. Ces différences sont relativement mineures. Par contre le rayonnement de surface total de surface est passé de 23% à 117% et une rétro-radiation de 100% qui serait provoquée par les gaz à effet de serre a été introduite. Les 117% correspondent à un rayonnement de 397 W/m2 qui a été calculé en considérant la Terre comme un corps noir à une température de 16 °C. Les 100 % de rétro-radiation ne sont là que pour conserver l’équilibre du bilan énergétique de surface.
Tout ceci est complètement incohérent.
Le diagramme de la NASA est similaire à la figure 1 dans (Trenberth, Fasullo, et Kiehl 2009) qui est une mise à jour d’une version de 1996 (Kiehl et Trenberth 1997).
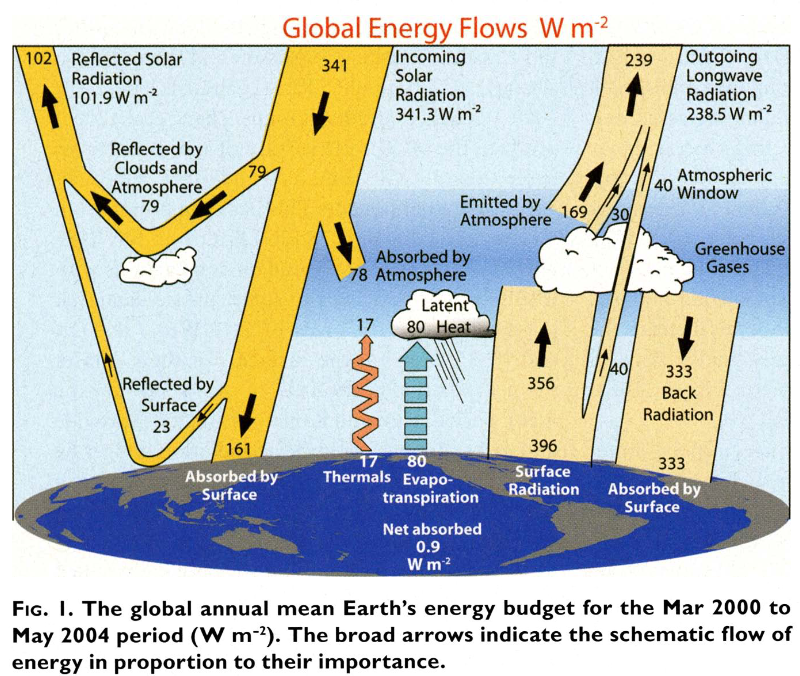
Les bilans sont équilibrés (à 1 W m^-2 près) aux niveaux du sol, de l’atmosphère et du sommet de l’atmosphère.
Le diagramme est établi sur base d’observations par satellite et d’un modèle informatique de radiation.
Ce modèle considère que la Terre est un corps noir qui a une température de 16 °C. La rayonnement de surface de 396 W m-2 a été calculé par l’Eq. 3 avec une température moyenne de 16 °C. Ce calcul est quasiment correct.
Considérons en effet que quelle que soit la longitude, le profil moyen de température selon un méridien soit de la forme suivante, x représentant la latitude en radians:

Dans ce profil, la température moyenne à l’équateur est égale à 28 °C et vaut -10 °C aux Pôles.
La moyenne de la température est égale à
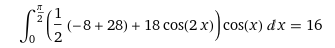
Le rayonnement moyen obtenu en appliquant l’Eq. 3 est égal à
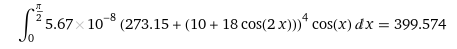
Si on fait le calcul inverse avec cette dernière valeur, on obtient une température correspondante de 16.6 °C.

Ces résultats sont très voisins de ceux du diagramme de Trenberth. L’inhomogénéité des températures n’introduit donc pas de fortes erreurs dans l’application de l’Eq. 3 à la surface de la sphère terrestre lorsqu’on tient compte implicitement de l’inertie thermique en utilisant un profil moyen de température valable quelle soit la longitude.
Un calcul plus précis que celui de Markus Ott montre que l’on retrouve facilement les températures observées en tenant compte de l’évaporation et de l’inertie thermique. Il se trouve ici.
5 Paléo-climatologie
Cet article publié sur SCE (2024.09.27) reprend 3 enregistrements paléo-climatiques intéressants: