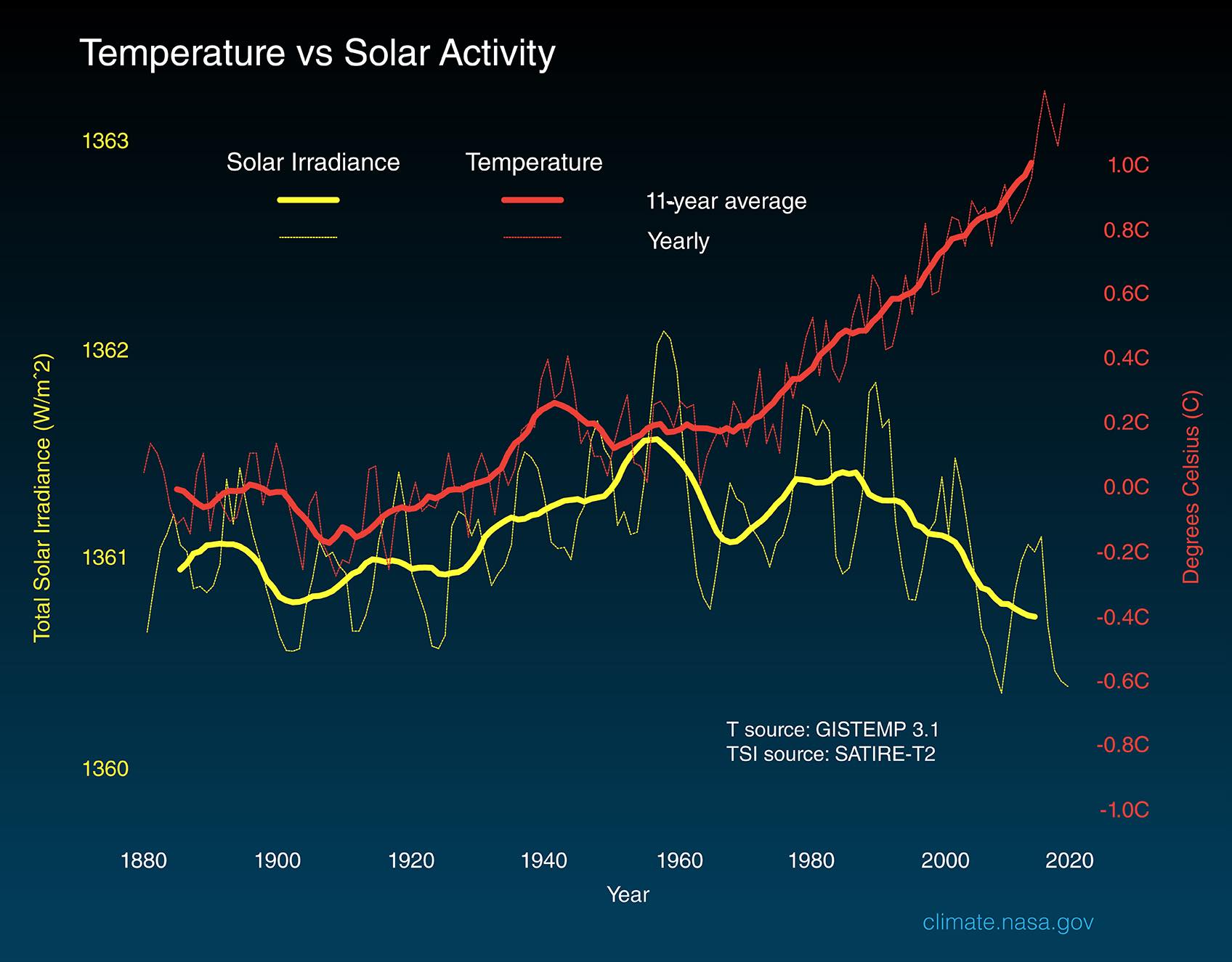
Température, rayonnement solaire et albedo

1 Introduction

Ce graphique publié par la NASA circule sans arrêt dans les milieux alarmistes climatiques.

Il serait la preuve irréfutable que le Soleil ne régit pas le climat puisque la température moyenne globale a augmenté alors que l’irradiance totale solaire (ITS) a diminué. Voir Fig. 1.

Fig. 1: Evolution de l’ITS et de la température moyenne globale selon la NASA.

Une telle affirmation n’est que le reflet d’une profonde méconnaissance des mécanismes qui gouvernent l’évolution de la température en fonction de l’activité solaire.

2 Un modèle thermique simple à la surface de la Planète

La masse océanique de la surface terrestre correspond à 300 fois celle de l’atmosphère, et sa capacité de stockage thermique représente 1000 fois celle de l’atmosphère. Voir ici.

La Terre absorbe de l’énergie en provenance du Soleil. Cette énergie s’accumule sous sa surface, ce qui tend à augmenter la température de surface. La chaleur accumulée est dissipée par la surface, ce qui a pour effet de diminuer la température.

Une équation différentielle très simple permet de modéliser ces mécanismes d’accumulation/dissipation. C’est expliqué de manière détaillée dans ce document.

Lorsque l’activité solaire varie de façon périodique, la température évolue également de façon périodique, mais avec un retard qui dépend de la fréquence de l’oscillation du rayonnement solaire et des caractéristiques thermiques du système.

Dans le cas d’oscillations lentes, le déphasage est nul, et il est égal au quart de la période pour des oscillations rapides. Voir ici.

Ce modèle thermique est à l’oeuvre en chaque point de la Planète. Il permet de comprendre pourquoi la température journalière passe par un maximum quelques heures après le passage du soleil au zénith. Pour la même raison, les extrema des températures saisonnières sont observés quelques semaines après les solstices.

Les cycles solaires présentent également une variation sinusoïdale, et on retrouve leurs empreintes dans le signal de la température avec un retard d’environ 2,75 ans qui est égal à la période moyenne de 11 ans des cycles solaires, divisée par 4, conformément à la théorie. Voir ici.

Une solution approchée de l’équation différentielle du modèle thermique peut être obtenue en se basant sur le rayonnement solaire moyenné sur un grand nombre d’années. Voir ici.

Le rayonnement solaire moyenné sur une centaine d’années, combiné à un terme harmonique d’assez faible amplitude et d’une période d’environ 66 ans produit une reconstruction fidèle des anomalies de température observées depuis 1850. Voir ici.

Le paradoxe apparent de la Fig. 1 se comprend aisément avec cet exercice de projection retrospective, mis au point pour tester les capacités prédictives du modèle. Même si le rayonnement solaire se stabilisait à sa valeur actuelle, sa valeur moyennée sur une centaine d’années continuerait à augmenter pendant une quarantaine d’années, ainsi que la température moyenne. Voir ici et ici .

3 Sensibilité de la température au rayonnement solaire absorbé et à l’albedo

Le GIEC prétend que l’augmentation de l’ITS depuis la fin du petit âge glaciaire ne peut en aucun cas justifier l’augmentation de température. Les reconstructions de l’ITS sont suffisamment longues pour calculer l’anomalie de température à partir de 1715. Ceci permet de faire une projection dans le passé qui donne une représentation très vraisemblable de la sortie du petit âge glaciaire. Voir ici.

Il existe plusieurs reconstructions de l’ITS. Certaines présentent une grande variabilité et d’autres une variabilité plus faible, tout en ayant la même allure. Du point de vue de la modélisation de l’anomalie de température, cela ne produit quasiment pas de différence parce que les analyses de régression non linéaires utilisées effectuent implicitement une translation et mise à échelle de telle manière que le profil temporel modélisé de l’anomalie de température est quasiment indépendant de la variabilité de la reconstruction de l’ITS.

Une reconstruction à faible variabilité (nrl2 du LISIRD) a été utilisée dans les analyses précédemment référencées. Depuis lors, le LISIRD a mis au point une nouvelle reconstruction de l’ITS qui présente encore beaucoup moins de variabilité. Les calculs faits avec cette nouvelle série produisent des résultats analogues, avec toutefois une perte de significativité dans les corrélations croisées. Pour une comparaison des 3 versions d’ITS du LISIRD, voir Section 4.1.1.

Le GIEC retient dans ses hypothèses une ITS à faible variabilité, et affirme qu’une augmentation d’ITS d’environ 1 W/M2 ne peut expliquer l’augmentation de température supérieure à 1 °C observée depuis 1850. Cette affirmation est fausse parce qu’elle suppose que l’albedo de la Planète reste constant.

Examinons comment la variation de température s’explique en cas de variation simultanée de l’albedo et du rayonnement solaire incident.

Soient:

$ϵ$	L’émissivité de la surface terrestre
$\sigma$	La constante de Stefan-Boltzmann (SB)
$k$	Le degré de transparence atmosphérique introduit dans le modèle à une couche.

Soient à un instant $t$ :

$S$	Le rayonnement solaire au sommet de l’atmosphère
$A$	L’albedo du système Terre-Atmosphère
$T$	La température de surface
$B$	$1-A$
$R$	Le rayonnement solaire absorbé = $(1+k)S/4$

Soient $S_0,A_0,T_0,B_0,R_0$ les valeurs de $S,A,T,B,R$ à un instant $t_0$.

Posons encore:

$\mathrm{\Delta }T$	$=T-T_0$
$\mathrm{\Delta }B$	$=B-B_0$
$\mathrm{\Delta }S$	$=S-S_0$
$\mathrm{\Delta }R$	$=R-R_0=(1+k)\mathrm{\Delta }S/4$

L’équilibre entre le rayonnement absorbé et la température selon la loi de SB, implique:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}\frac{S(1-A)(1+k)}{4}& =ϵ\sigma T^4\\ RB& =ϵ\sigma T^4\end{array}\end{array}$$

En linéarisant le terme $T^4$,

$$\begin{array}{}\text{(2)}& \begin{array}{rl}(R_0+\mathrm{\Delta }R)(B_0+\mathrm{\Delta }B)& =ϵ\sigma (T_0+\mathrm{\Delta }T{)}^4\\ & \approx ϵ\sigma (T_0^4+4T_0^3\mathrm{\Delta }T)\\ R_0{B}_0+R_0\mathrm{\Delta }B+B_0\mathrm{\Delta }R+\mathrm{\Delta }R\mathrm{\Delta }B& \approx ϵ\sigma T_0^4+ϵ\sigma 4T_0^3\mathrm{\Delta }T\end{array}\end{array}$$

En notant que

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{R}_0{B}_0& =ϵ\sigma T_0^4\\ \mathrm{\Delta }R\mathrm{\Delta }B& \approx 0\end{array}\end{array}$$

Il vient:

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{R}_0{B}_0\frac{\mathrm{\Delta }B}{B_0}+R_0{B}_0\frac{\mathrm{\Delta }R}{R_0}& \approx 4R_0{B}_0\frac{\mathrm{\Delta }T}{T_0}\\ \frac{\mathrm{\Delta }T}{T_0}& \approx \frac{1}{4}(\frac{\mathrm{\Delta }B}{B_0}+\frac{\mathrm{\Delta }R}{R_0})\end{array}\end{array}$$

Si l’albedo est constant, $\mathrm{\Delta }B=0$, et

$$\begin{array}{}\text{(5)}& \begin{array}{rl}\frac{\mathrm{\Delta }T}{T_0}& \approx \frac{1}{4}(\frac{\mathrm{\Delta }R}{R_0})\approx \frac{1}{4}(\frac{\mathrm{\Delta }S}{S_0})\end{array}\end{array}$$

Si l’ITS augmente de $\mathrm{\Delta }S=1W/M2$, avec $S_0=1360W/M2$ et $T_0=288°K$, on a $\mathrm{\Delta }T\approx 0.05°K$. Cette valeur est effectivement négligeable, et une série d’ITS à haute variabilité ne pourra expliquer l’augmentation de température de plus de 1 °C depuis 1850.

Si le rayonnement solaire est constant, alors $\mathrm{\Delta }R=0$, et

$$\begin{array}{rl}\frac{\mathrm{\Delta }T}{T_0}& \approx \frac{1}{4}(\frac{\mathrm{\Delta }B}{B_0})\end{array}$$

On pourrait observer des variations de température si des oscillations océaniques ou des variations d’activité géothermique étaient actives dans les régions polaires, en l’absence de variation du rayonnement solaire.

En supposant que $\mathrm{\Delta }B$ soit proportionnel à $\mathrm{\Delta }T$, on peut exprimer la variation de température en fonction de la variation du rayonnement absorbé et mettre en évidence un facteur d’amplification de la variation de température causé par la variation d’albedo:

$$\begin{array}{}\text{(6)}& \begin{array}{rl}\mathrm{\Delta }B& =\beta \mathrm{\Delta }T\\ 4\frac{\mathrm{\Delta }T}{T_0}& \approx \frac{\beta \mathrm{\Delta }T}{B_0}+\frac{\mathrm{\Delta }R}{R_0}\\ 4\frac{\mathrm{\Delta }T}{T_0}& \approx \frac{\beta \mathrm{\Delta }T{T}_0}{T_0{B}_0}+\frac{\mathrm{\Delta }R}{R_0}\\ (4-\frac{\beta T_0}{B_0})\frac{\mathrm{\Delta }T}{T_0}& \approx \frac{\mathrm{\Delta }R}{R_0}\\ \frac{\mathrm{\Delta }T}{T_0}& \approx \frac{\mathrm{\Delta }R}{R_0}\frac{1}{(4-\frac{\beta T_0}{B_0})}\\ \frac{\mathrm{\Delta }T}{T_0}& \approx \frac{1}{4}\frac{\mathrm{\Delta }R}{R_0}\frac{1}{(1-\frac{\beta T_0}{4B_0})}\\ \frac{(\frac{\mathrm{\Delta }T}{T_0}{)}_{\beta \ne 0}}{(\frac{\mathrm{\Delta }T}{T_0}{)}_{\beta =0}}& \approx \frac{1}{(1-\frac{\beta T_0}{4B_0})}\end{array}\end{array}$$

Ce facteur d’amplification est implicitement compris dans les coefficients de la régression non-linéaire du modèle thermique.

Il est difficile de l’évaluer parce que l’albedo global dépend de la part de rayonnement solaire réfléchie par les nuages et de celle réfléchie par la surface.

Les reconstructions climatiques (CERES et ERA5) permettent de calculer un albedo au sommet de l’atmosphère et un albedo au niveau de la surface.

Des analyses de régression linéaire permettent d’estimer l’influence du rayonnement et des albedos sur la température.

4 Température, rayonnement solaire et albedos

4.1 Données de base

Les séries temporelles des reconstruction CERES et ERA5 analyses ont été désaisonnalisées pour effectuer les analyses. Les reconstructions de l’ITS du LISIRD ont été utilisées pour moyenner l’ITS sur un grand nombre d’années, parce que les reconstructions CERES et ERA5 sont trop courtes.

4.1.1 TSI/4 (LISIRD)

Fig. 2: Trois versions de l’ITS publiées par le LISIRD, ainsi que leurs moyennes sur une centaine d’années. Les valeurs ont été divisées par 4 pour les ramener à leurs moyennes sur le disque planétaire.

La version la plus ancienne (hist) a été arrêtée en 2018. Elle a été remplacée par la version nrl2 arrêtée en 2021, présentée à l’époque comme le nec plus ultra. Ces deux versions présentaient une faible variabilité. La dernière mouture présente une variabilité deux fois plus faible. Des changements aussi rapides laissent planer un doute sur leurs motivations et leur crédibilité.

La version nnl semble être la base reprise dans les reconstructions CERES et ERA5, mais des différences sont à noter.

4.1.2 Rayonnement solaire incident

Fig. 3: Les très fortes valeurs de rayonnement CERES et LISIRD des dernières années peuvent poser question. Elles ne sont pas corroborées par les observations des taches solaires du SIDC.

4.1.3 Albedo au sommet de l’atmosphère

Fig. 4: Les versions CERES et ERA5 se ressemblent. Toutefois, la version CERES est en diminution constante depuis l’an 2000, alors que la version ERA5 est en baisse depuis seulement 2010.

4.1.4 Albedo en surface

Fig. 5: Les albedos de surface CERES et ERA5 ont la même allure.

4.1.5 Températures

Fig. 6: Les températures NCEP et ERA5 ont évolué en parrallèle jusqu’en 2016, pour se rejoindre par la suite.

4.2 Analyses de régression

Différentes analyses de régression ont été menées pour modéliser l’anomalie de température à 2 m en fonction des anomalies de rayonnement, et des albedos (au sommet de l’atmosphère, et en surface). Toutes les combinaisons possibles de variables indépendantes ont été évaluées.

Les anomalies ont été calculées en se basant sur la moyenne des variables pendant la fenêtre temporelle d’observation.

La reconstruction CERES qui ne contient que des rayonnements a été complétée par la température à 2 m venant de la reconstruction NCEP.

Les mêmes analyses ont été réalisées pour les reconstructions CERES et ERA5.

Les résultats sont repris dans la Table 1. La Table 2 reprend les noms et descriptions des variables utilisées dans les régressions.

Table 1: Synthèse des analyses de régression

Formule de régression	Adjusted Rsquared (CERES)	Adjusted Rsquared (ERA5)
t2m = a1	0.0165	0.0099
t2m = a2	-0.0033	-0.0010
t2m = a3	0.3023	0.8180
t2m = b	0.7264	0.0094
t2m = c	0.7549	0.8804
t2m = a3 + b	0.7479	0.8382
t2m = a3 + c	0.8141	0.9172
t2m = b + c	0.7778	0.8806
t2m = a3 + b + c	0.8173	0.9203

Table 2: Noms et descriptions des variables

Nom variable	Description
t2m	L’anomalie de température à 2 m
a1	L’anomalie de l’ITS divisée par 4 de la reconstruction CERES ou ERA5
a2	L’anomalie de l’ITS divisée par 4 ( série nnl du LISIRD)
a3	La valeur de a2 moyennée sur une centaine d’années
b	L’anomalie de l’albédo au sommet de l’atmosphère
c	L’anomalie de l’albédo de surface

La régression t2m = a3 + c a été mise en graphique pour la reconstruction CERES (Fig. 7) et pour la reconstruction ERA5 (Fig. 8).

Fig. 7

Fig. 8

Il y a une forte corrélation entre l’albédo de surface ERA5 et le rayonnement solaire moyenné du LISIRD. Voir Fig. 9.

Fig. 9

Il y a également une forte corrélation entre l’albédo de surface et la température à 2m (ERA5). Voir Fig. 10.

Fig. 10

5 Conclusions

Il n’y a aucune corrélation entre le rayonnement solaire instantané (a1 ou a2) et la température (t2m).

Il y a une corrélation beaucoup plus forte entre le rayonnement solaire moyenné sur une centaine d’années (a3) et la température (t2m), bien qu’elle soit moins marquée dans le cas CERES. Ceci conforte le modèle thermique, même avec une série d’ITS à très faible variabilité.

L’albedo au sommet de l’atmosphère (b) est peu corrélé avec la température (t2m) dans le cas ERA5. Il y a une corrélation assez marquée dans le cas CERES, mais cette reconstruction est beaucoup plus courte. Il est fort possible que cette corrélation disparaîtrait si cette série était plus longue.

Il y a une très forte corrélation entre l’albedo de surface (c) et la température (t2m). Cette corrélation est plus forte que celle entre le rayonnement solaire moyenné (a3) et la température (t2m).

La corrélation t2m = b + c n’est que marginalement meilleure par rapport à la corrélation t2m = c.

La corrélation t2m = a3 + c est excellente, elle n’est que marginalement moins bonne que la corrélation t2m = a3 + b + c.

Au terme de ces analyses, on peut considérer que la relation de causalité est la suivante: le rayonnement solaire moyenné provoque une augmentation de température qui induit une diminution de l’albedo qui amplifie l’augmentation de température. Il est en effet difficile d’imaginer que la diminution d’albedo soit la cause primaire de l’augmentation de température, ce qui en ferait également la cause de l’augmentation du rayonnement solaire moyenné.

6 Annexe: détail des analyses de régression

6.1 Avec les données CERES

6.1.1 regr_CERES_t2m_a1

Call:
lm(formula = air_t_d ~ inc_sol_t_d, data = comm_CERES_df)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.39817 -0.10876 -0.01129  0.11825  0.31774 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)  
(Intercept) -1.179e-14  9.237e-03   0.000   1.0000  
inc_sol_t_d  2.130e-01  8.779e-02   2.426   0.0159 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1578 on 290 degrees of freedom
Multiple R-squared:  0.01989,   Adjusted R-squared:  0.01651 
F-statistic: 5.885 on 1 and 290 DF,  p-value: 0.01588

6.1.2 regr_CERES_t2m_a2

Call:
lm(formula = air_t_d ~ tsi4_d, data = comm_CERES_df)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.38033 -0.10958 -0.01877  0.11016  0.31468 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)
(Intercept) -6.418e-15  9.330e-03   0.000    1.000
tsi4_d       1.821e-02  9.685e-02   0.188    0.851

Residual standard error: 0.1594 on 290 degrees of freedom
Multiple R-squared:  0.0001219, Adjusted R-squared:  -0.003326 
F-statistic: 0.03537 on 1 and 290 DF,  p-value: 0.851

6.1.3 regr_CERES_t2m_a3

Call:
lm(formula = air_t_d ~ tsi4_ma_d, data = comm_CERES_df)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.32429 -0.07250  0.02026  0.08866  0.26446 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 1.052e-12  7.780e-03    0.00        1    
tsi4_ma_d   4.987e+01  4.424e+00   11.27   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1329 on 290 degrees of freedom
Multiple R-squared:  0.3047,    Adjusted R-squared:  0.3023 
F-statistic: 127.1 on 1 and 290 DF,  p-value: < 2.2e-16

6.1.4 regr_CERES_t2m_b

Call:
lm(formula = air_t_d ~ toa_alb_t_d, data = comm_CERES_df)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.161684 -0.068264  0.007745  0.050840  0.219392 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -4.475e-15  4.872e-03    0.00        1    
toa_alb_t_d -7.440e+01  2.675e+00  -27.82   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.08325 on 290 degrees of freedom
Multiple R-squared:  0.7274,    Adjusted R-squared:  0.7264 
F-statistic: 773.7 on 1 and 290 DF,  p-value: < 2.2e-16

6.1.5 regr_CERES_t2m_c

Call:
lm(formula = air_t_d ~ sfc_alb_t_d, data = comm_CERES_df)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.21409 -0.05207  0.01598  0.05107  0.15400 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -6.836e-15  4.611e-03    0.00        1    
sfc_alb_t_d -9.752e+01  3.255e+00  -29.96   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.07879 on 290 degrees of freedom
Multiple R-squared:  0.7558,    Adjusted R-squared:  0.7549 
F-statistic: 897.4 on 1 and 290 DF,  p-value: < 2.2e-16

6.1.6 regr_CERES_t2m_a3b

Call:
lm(formula = air_t_d ~ tsi4_ma_d + toa_alb_t_d, data = comm_CERES_df)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.165638 -0.071668  0.006745  0.051713  0.202678 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  3.248e-13  4.677e-03   0.000        1    
tsi4_ma_d    1.553e+01  3.060e+00   5.073 7.01e-07 ***
toa_alb_t_d -6.697e+01  2.955e+00 -22.664  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.07991 on 289 degrees of freedom
Multiple R-squared:  0.7497,    Adjusted R-squared:  0.7479 
F-statistic: 432.7 on 2 and 289 DF,  p-value: < 2.2e-16

6.1.7 regr_CERES_t2m_a3c

Call:
lm(formula = air_t_d ~ tsi4_ma_d + sfc_alb_t_d, data = comm_CERES_df)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.178614 -0.042373  0.003905  0.048528  0.140064 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  4.980e-13  4.016e-03    0.00        1    
tsi4_ma_d    2.379e+01  2.463e+00    9.66   <2e-16 ***
sfc_alb_t_d -8.646e+01  3.058e+00  -28.27   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.06862 on 289 degrees of freedom
Multiple R-squared:  0.8154,    Adjusted R-squared:  0.8141 
F-statistic: 638.2 on 2 and 289 DF,  p-value: < 2.2e-16

6.1.8 regr_CERES_t2m_bc

Call:
lm(formula = air_t_d ~ toa_alb_t_d + sfc_alb_t_d, data = comm_CERES_df)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.175633 -0.057231  0.007595  0.054875  0.170935 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -5.856e-15  4.391e-03   0.000        1    
toa_alb_t_d -3.170e+01  5.710e+00  -5.551 6.42e-08 ***
sfc_alb_t_d -6.057e+01  7.343e+00  -8.248 5.75e-15 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.07503 on 289 degrees of freedom
Multiple R-squared:  0.7793,    Adjusted R-squared:  0.7778 
F-statistic: 510.3 on 2 and 289 DF,  p-value: < 2.2e-16

6.1.9 regr_CERES_t2m_a3bc

Call:
lm(formula = air_t_d ~ tsi4_ma_d + toa_alb_t_d + sfc_alb_t_d, 
    data = comm_CERES_df)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.165701 -0.046853  0.008009  0.047352  0.144053 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  4.434e-13  3.982e-03   0.000   1.0000    
tsi4_ma_d    2.120e+01  2.661e+00   7.967 3.82e-14 ***
toa_alb_t_d -1.383e+01  5.643e+00  -2.451   0.0149 *  
sfc_alb_t_d -7.154e+01  6.800e+00 -10.521  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.06804 on 288 degrees of freedom
Multiple R-squared:  0.8192,    Adjusted R-squared:  0.8173 
F-statistic: 434.9 on 3 and 288 DF,  p-value: < 2.2e-16

6.2 Avec les données ERA5

6.2.1 regr_ERA5_t2m_a1

Call:
lm(formula = t2m_t_d ~ tisr_t_d, data = comm_ERA5_df)

Residuals:
    Min      1Q  Median      3Q     Max 
-0.5510 -0.2995 -0.1063  0.2856  1.1112 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.682e-14  1.154e-02   0.000 1.000000    
tisr_t_d     4.572e-01  1.371e-01   3.335 0.000884 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.3674 on 1012 degrees of freedom
Multiple R-squared:  0.01087,   Adjusted R-squared:  0.009893 
F-statistic: 11.12 on 1 and 1012 DF,  p-value: 0.0008844

6.2.2 regr_ERA5_t2m_a2

Call:
lm(formula = t2m_t_d ~ tsi4_d, data = comm_ERA5_df)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.51985 -0.30847 -0.09878  0.29812  1.08004 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.224e-14  1.160e-02   0.000    1.000
tsi4_d       2.334e-02  1.336e-01   0.175    0.861

Residual standard error: 0.3694 on 1012 degrees of freedom
Multiple R-squared:  3.017e-05, Adjusted R-squared:  -0.0009579 
F-statistic: 0.03054 on 1 and 1012 DF,  p-value: 0.8613

6.2.3 regr_ERA5_t2m_a3

Call:
lm(formula = t2m_t_d ~ tsi4_ma_d, data = comm_ERA5_df)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.31482 -0.11391 -0.01312  0.12383  0.40343 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -9.576e-14  4.946e-03    0.00        1    
tsi4_ma_d    5.481e+01  8.121e-01   67.49   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1575 on 1012 degrees of freedom
Multiple R-squared:  0.8182,    Adjusted R-squared:  0.818 
F-statistic:  4555 on 1 and 1012 DF,  p-value: < 2.2e-16

6.2.4 regr_ERA5_t2m_b

Call:
lm(formula = t2m_t_d ~ toa_alb_t_d, data = comm_ERA5_df)

Residuals:
    Min      1Q  Median      3Q     Max 
-0.5318 -0.2967 -0.1333  0.2839  1.1315 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)   
(Intercept) -2.204e-14  1.154e-02    0.00  1.00000   
toa_alb_t_d  2.160e+01  6.647e+00    3.25  0.00119 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.3675 on 1012 degrees of freedom
Multiple R-squared:  0.01033,   Adjusted R-squared:  0.009351 
F-statistic: 10.56 on 1 and 1012 DF,  p-value: 0.001192

6.2.5 regr_ERA5_t2m_c

Call:
lm(formula = t2m_t_d ~ sfc_alb_t_d, data = comm_ERA5_df)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.33047 -0.08747  0.00186  0.08582  0.33840 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.938e-14  4.011e-03    0.00        1    
sfc_alb_t_d -1.984e+02  2.298e+00  -86.34   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1277 on 1012 degrees of freedom
Multiple R-squared:  0.8805,    Adjusted R-squared:  0.8804 
F-statistic:  7455 on 1 and 1012 DF,  p-value: < 2.2e-16

6.2.6 regr_ERA5_t2m_a3b

Call:
lm(formula = t2m_t_d ~ tsi4_ma_d + toa_alb_t_d, data = comm_ERA5_df)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.29563 -0.11964 -0.01104  0.11264  0.35968 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -9.904e-14  4.663e-03    0.00        1    
tsi4_ma_d    5.718e+01  7.939e-01   72.02   <2e-16 ***
toa_alb_t_d -3.145e+01  2.785e+00  -11.29   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1485 on 1011 degrees of freedom
Multiple R-squared:  0.8386,    Adjusted R-squared:  0.8382 
F-statistic:  2626 on 2 and 1011 DF,  p-value: < 2.2e-16

6.2.7 regr_ERA5_t2m_a3c

Call:
lm(formula = t2m_t_d ~ tsi4_ma_d + sfc_alb_t_d, data = comm_ERA5_df)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.31908 -0.06849 -0.00987  0.07877  0.28137 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -5.090e-14  3.336e-03    0.00        1    
tsi4_ma_d    2.276e+01  1.071e+00   21.25   <2e-16 ***
sfc_alb_t_d -1.302e+02  3.736e+00  -34.84   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1062 on 1011 degrees of freedom
Multiple R-squared:  0.9174,    Adjusted R-squared:  0.9172 
F-statistic:  5613 on 2 and 1011 DF,  p-value: < 2.2e-16

6.2.8 regr_ERA5_t2m_bc

Call:
lm(formula = t2m_t_d ~ toa_alb_t_d + sfc_alb_t_d, data = comm_ERA5_df)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.33218 -0.08582  0.00211  0.08676  0.33599 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.938e-14  4.006e-03   0.000   1.0000    
toa_alb_t_d  4.187e+00  2.316e+00   1.808   0.0709 .  
sfc_alb_t_d -1.980e+02  2.304e+00 -85.948   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1276 on 1011 degrees of freedom
Multiple R-squared:  0.8809,    Adjusted R-squared:  0.8806 
F-statistic:  3737 on 2 and 1011 DF,  p-value: < 2.2e-16

6.2.9 regr_ERA5_t2m_a3bc

Call:
lm(formula = t2m_t_d ~ tsi4_ma_d + toa_alb_t_d + sfc_alb_t_d, 
    data = comm_ERA5_df)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.277384 -0.071895 -0.007365  0.079230  0.246818 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -5.458e-14  3.274e-03   0.000        1    
tsi4_ma_d    2.540e+01  1.132e+00  22.436  < 2e-16 ***
toa_alb_t_d -1.281e+01  2.039e+00  -6.283 4.93e-10 ***
sfc_alb_t_d -1.233e+02  3.824e+00 -32.257  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1043 on 1010 degrees of freedom
Multiple R-squared:  0.9205,    Adjusted R-squared:  0.9203 
F-statistic:  3897 on 3 and 1010 DF,  p-value: < 2.2e-16

6.2.10 regr_ERA5_c_a3

Call:
lm(formula = sfc_alb_t_d ~ tsi4_ma_d, data = comm_ERA5_df)

Residuals:
       Min         1Q     Median         3Q        Max 
-0.0018477 -0.0006394 -0.0001650  0.0007780  0.0021800 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  3.447e-16  2.807e-05    0.00        1    
tsi4_ma_d   -2.463e-01  4.609e-03  -53.44   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.0008938 on 1012 degrees of freedom
Multiple R-squared:  0.7383,    Adjusted R-squared:  0.7381 
F-statistic:  2855 on 1 and 1012 DF,  p-value: < 2.2e-16

6.2.11 regr_ERA5_c_t2m

Call:
lm(formula = sfc_alb_t_d ~ t2m_t_d, data = comm_ERA5_df)

Residuals:
       Min         1Q     Median         3Q        Max 
-1.578e-03 -4.101e-04  4.093e-05  3.815e-04  1.797e-03 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -8.439e-17  1.897e-05    0.00        1    
t2m_t_d     -4.438e-03  5.141e-05  -86.34   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.0006041 on 1012 degrees of freedom
Multiple R-squared:  0.8805,    Adjusted R-squared:  0.8804 
F-statistic:  7455 on 1 and 1012 DF,  p-value: < 2.2e-16