DRAFT - Le modèle à une couche étendu

Le b.a. ba de l’effet de serre … thermique et non de fluorescence

Dans le modèle à une couche, l’effet de serre est expliqué par l’interaction de deux plaques qui se comportent comme des corps noirs. Ce modèle est enseigné dans différentes universités et diffusé par des institutions académiques. Il est considéré comme le b.a-ba de l’effet de serre. Voir par exemple (Dufresne et Treiner 2011).

Ce modèle produit des valeurs trop élevées de température de surface. Un paramètre k décrivant le degré de transparence de l’atmosphère est introduit. Il permet d’ajuster ce modèle aux observations. Voir Fig. 1.

Soient

$S$	Le rayonnement solaire au sommet de l’atmosphère	1368 W m-2
$A$	L’albédo de la Planète	0.3
$S_a=(1-A)S/4$	Le rayonnement solaire moyen absorbé par la surface terrestre	239 W m-2
${ϵ}_S$	L’émissivité de la surface terrestre
${ϵ}_A$	L’émissivité de l’atmosphère
$\sigma$	La constante de Stefan-Boltzmann (SB)	5.67 10-8 W m-2 °K-4
$T_{S0}$	La température de la surface terrestre en l’absence d’atmosphère	255 °K
$T_{S1}$	La température de la surface terrestre en présence d’une atmosphère	292 °K
$T_A$	La température moyenne d’une atmosphère concentrée en une seule couche	K
$R_{S0}$	Le rayonnement émis par la surface terrestre en l’absence d’atmosphère
$R_{S1}$	Le rayonnement émis par la surface terrestre en présence d’une atmosphère
$R_A$	Le rayonnement émis par l’atmosphère vers le haut et vers le bas
$k$	Le degré de transparence de l’atmosphère	$0<=k<=1$

Note: La valeur $T_{S1}=292°K$ est la valeur actuelle de la température de moyenne de surface des océans (série temporelle NOAA OI V2)

Fig. 1: Le volet A correspond à une Terre sans atmosphère. La surface terrestre est assimilée à un corps noir/gris dont la face inférieure est parfaitement isolée (rectangle noir). Dans le volet B, l’atmosphère est assimilée à une vitre (rectangle bleu). Cette vitre est un corps noir/gris partiellement transparent au rayonnement solaire, mais opaque au rayonnement IR émis par la surface terrestre.

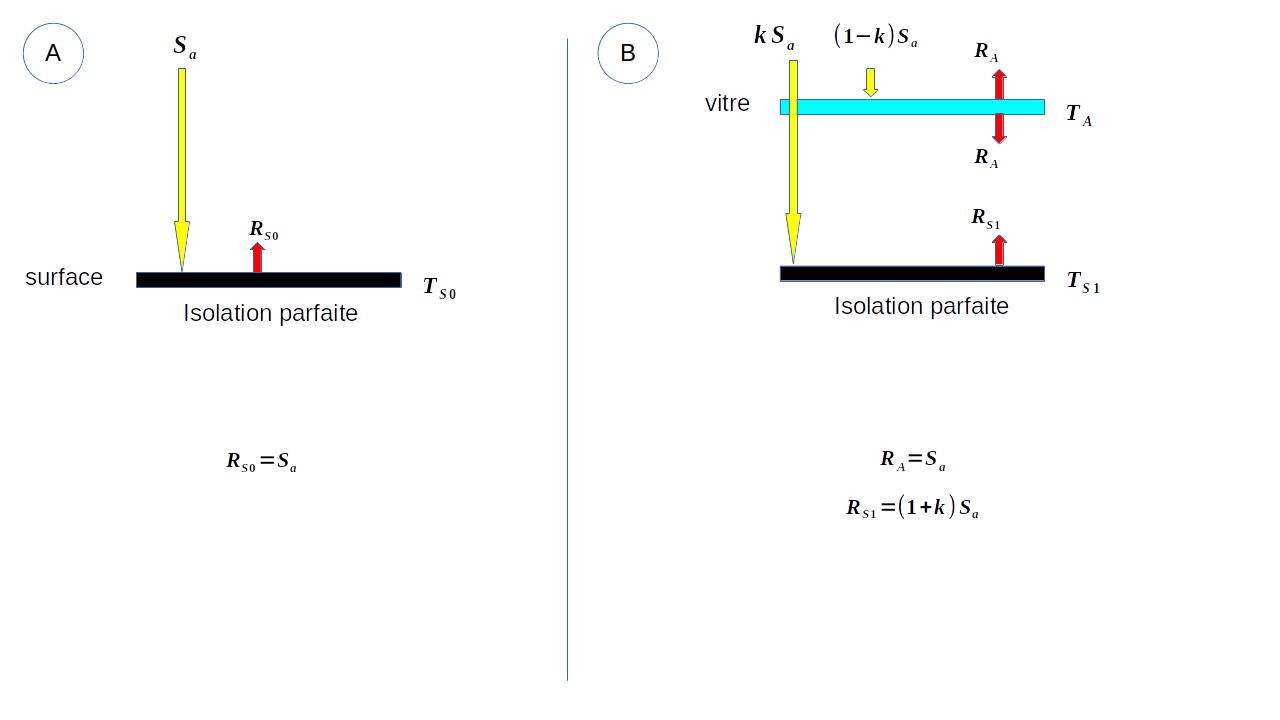
Pour une Terre corps noir sans atmosphère, le bilan thermique s’écrit (flux reçu = flux émis):

$$\begin{array}{}\text{(1)}& S_a=R_{S0}={ϵ}_S\sigma T_{S0}^4\end{array}$$

On en déduit

$$\begin{array}{}\text{(2)}& T_{S0}=\sqrt[4]{\frac{S_a}{{ϵ}_S\sigma }}\end{array}$$

Pour une Terre avec atmosphère, il faut écrire le bilan thermique de chaque plaque.

Pour la surface terrestre on a:

$$\begin{array}{}\text{(3)}& k{S}_a+R_A=R_{S1}\end{array}$$

D’une manière analogue, on a pour l’atmosphère:

$$\begin{array}{}\text{(4)}& \begin{array}{rl}(1-k)S_a+R_{S1}& =2R_A\\ \frac{1}{2}[(1-k)S_a+R_{S1}]& =R_A\end{array}\end{array}$$

En injectant l’Eq. 4 dans l’Eq. 3, il vient

$$\begin{array}{}\text{(5)}& k{S}_a+\frac{1}{2}[(1-k)S_a+\sigma T_{S1}^4]=\sigma T_{S1}^4\end{array}$$

Et donc

$$\begin{array}{}\text{(6)}& R_{S1}=(1+k)S_a\end{array}$$

En injectant cette valeur dans l’Eq. 3, on obtient

$$\begin{array}{}\text{(7)}& R_A=S_a\end{array}$$

$R_A$ et $R_{S1}$ ne dépendent pas des émissivités et $R_A$ ne dépend pas du degré de transparence $k$.

Les températures s’obtiennent en appliquant la loi de SB.

Pour la surface:

$$\begin{array}{}\text{(8)}& \begin{array}{rl}{T}_{S1}& =\sqrt[4]{1+k}\sqrt[4]{\frac{S_a}{{ϵ}_S\sigma }}\\ & =\sqrt[4]{1+k}{T}_{S0}\end{array}\end{array}$$

La valeur de $T_{S1}$ est la plus grande lorsque $k=1$.

Pour l’atmosphère:

$$\begin{array}{}\text{(9)}& T_A=\sqrt[4]{\frac{S_a}{{ϵ}_A\sigma }}\end{array}$$

Pour une atmosphère complètement transparente, $k=1$ et une émissivité ${ϵ}_S$ de 1, et on retrouve la valeur publiée dans Dufresne et Treiner (2011):

$$T_{S1}=\sqrt[4]{2}{T}_{S0}=303°K$$

Cette valeur est sensiblement supérieure aux observations.

Avec la température moyenne observée de 292 °C et une valeur communément admise ${ϵ}_S=0.97$, le rayonnement émis par la surface $R_{S1}=400W/M^2$. Par l’Eq. 6, on en déduit $k=400/239-1=0.673$. La part de rayonnement solaire absorbée par l’atmosphère vaut $(1-0.673)\ast 239=78W/M^2$. On retrouve exactement ces chiffres dans le diagramme de Trenberth qui les a établis par une approche plus compliquée et tout à fait différente!! Voir la Fig. 2 extraite de Trenberth, Fasullo, et Kiehl (2009).

Fig. 2: Diagramme de Trenberth

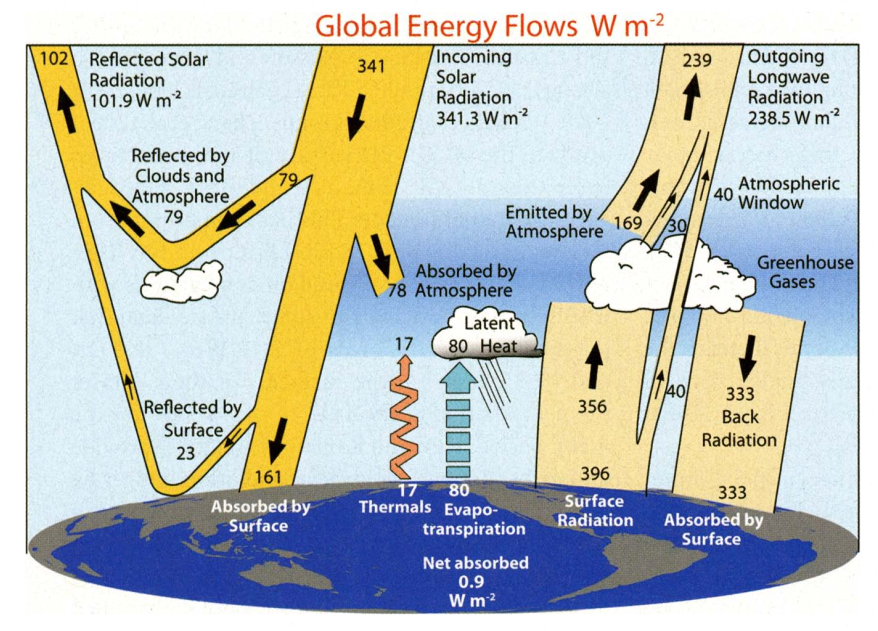
Dans ce modèle, la rétro-radiation est égale au rayonnement solaire moyen absorbé, à savoir 239 W/M² , indépendamment de la valeur de $k$. Elle est de nature thermique. C’est un rayonnement de corps noir/gris suivant la loi de SB causé par les oscillations de dipôles électriques au sein de la matière. Ce rayonnement n’a rien à voir avec le rayonnement de fluorescence caractéristique des gaz à effet de serre (GES).

Dans l’atmosphère, seule l’eau liquide ou solide présente dans les nuages est capable d’émettre un rayonnement thermique de type SB. Les molécules de GES autres que l’eau n’existent que sous forme gazeuse dans l’atmosphère. Les molécules gazeuses n’émettent pas de rayonnement thermique.

L’interprétation du diagramme de Trenberth à la lumière de ce modèle thermique se trouve ici.

Un calcul des températures de surface au moyen de ce modèle se trouve ici.

Dans Dufresne et Treiner (2011), l’effet d’une augmentation des GES est simulé en augmentant le nombre de plaques. Dans un modèle à n plaques isothermes, la température de celle du dessus est inchangée, et celle du dessous augmente indéfiniment avec le nombre de plaques. Il en va de même pour le gradient de température entre la première et la dernière plaque, qui n’a rien à voir avec le gradient adiabatique observé dans la troposphère. Ce modèle à N plaques est complètement irréaliste.

Dans la Fig. 1, si on introduisait de l’air contenant des GES entre les deux plaques, chaque plaque serait soumise à une rétro-radiation et devrait donc se réchauffer. Dans ce cas, le bilan énergétique ne serait plus équilibré. Il est impossible que les GES qui n’ont aucun pouvoir réchauffant puisse créer un tel déséquilibre. Le bilan énergétique de chaque plaque ne peut changer. Pour chaque plaque, la rétro-radiation sera soit absorbée et réémise, soit réfléchie, mais sans changement de température.

La nature essentiellement thermique de la rétro-radiation est décrite dans les sections 5.4.1 et 5.4.2 dans Monteith et Unsworth (2013). La formule 5.30 qui y est proposée pour estimer la rétro-radiation est très explicite:

Dans une étude exhaustive de la rétro-radiation (Tian et al. (2023)) basée sur les observations FLUXNET, le jeu de données NASA-CERES et la réanalyse ERA5, les auteurs arrivent à la conclusion que la chaleur accumulée dans la basse atmosphère est la principale source des variations diurnes et saisonnières de la rétro-radiation. Les formules 3, 4, 5 qu’ils utilisent dans leurs analyses et qui produisent d’excellentes corrélations, ne laissent planer aucun doute: la basse atmosphère se comporte comme un corps gris.

Les références

Dufresne, Jean-Louis, et Jacques Treiner. 2011. « L’effet de serre atmosphérique: plus subtil qu’on ne le croit! » Le Bup 105 (936): 821‑40. https://www.hprevot.fr/plus-subtil.pdf.

Monteith, John, et Mike Unsworth. 2013. Principles of environmental physics: plants, animals, and the atmosphere. Academic press. https://dlib.scu.ac.ir/bitstream/Hannan/388077/2/9780123869104.pdf.

Tian, Yinglin, Deyu Zhong, Sarosh Alam Ghausi, Guangqian Wang, et Axel Kleidon. 2023. « Understanding variations in downwelling longwave radiation using Brutsaert’s equation ». Earth System Dynamics 14 (6): 1363‑74. https://esd.copernicus.org/articles/14/1363/2023/esd-14-1363-2023.pdf.

Trenberth, Kevin E, John T Fasullo, et Jeffrey Kiehl. 2009. « Earth’s global energy budget ». Bulletin of the american meteorological society 90 (3): 311‑24. https://journals.ametsoc.org/view/journals/bams/90/3/2008bams2634_1.xml.